Han sido tres siglos los necesarios para llegar a estas definiciones desde que Jonh Wallis (1616-1703) formulase la que es aceptada como la primera en el siglo XVII. Él fue el primero que estableció claramente la noción de límite en la forma rigurosa hoy vigente, esto es, con la condición de que la diferencia entre la variable y el límite sea “quavis asignabilis minor”.
Fue Augustin Louis Cauchy (1789-1848) quien puso los cimientos del análisis infinitesimal fundamentando el cálculo sobre el concepto de límite, siguiendo los criterios que ya apuntaron anteriormente John Wallis y James Gregory en el S.XVI I y ya en el siglo siguiente Jean Le Rond d’Alembert había incluido en la famosa enciclopedia francesa Encyclopédie una entrada para el concepto de Límite, que es definido como:
“Se dice que una cantidad es el límite de otra cantidad cuando la segunda puede aproximarse a la primera con una diferencia menor que cualquier cantidad dada, por pequeña que esta se pueda suponer, aunque la cantidad que se aproxima no pueda sobrepasar nunca la cantidad aproximada. (…) La teoría de límites –agregaba d’Alembert—es la base de la verdadera metafísica del cálculo diferencial.”
Habría que esperar hasta el año 1821 cuando apareció finalmente el famoso texto de Cauchy titulado Cours d’analyse algébrique, que refundaba la metodología matemática sobre bases conceptuales estrictamente rigurosas, en el ámbito del cálculo infinitesimal. En esta obra, el autor francés establecía cuidadosamente las nociones básicas del cálculo: función, límite, continuidad, derivada e integral. También distinguía allí entre las series infinitas sumables y las no sumables, es decir, entre series convergentes y divergentes.
En su obra Cauchy definía el límite de una función de la siguiente forma:
“Cuando los valores atribuidos sucesivamente a una variable se aproximan indefinidamente a un valor fijo para llegar por último a diferir de este valor en una cantidad tan pequeña como se desee, entonces dicho valor fijo recibe el nombre de límite de todos los demás valores.”
Como se puede comprobar la definición no estaba totalmente pulida, tendrían que pasar aún unos treinta años para que el riguroso alemán Karl Weierstrass viniese a rematar la faena del delicado concepto de límite, con la ayuda de sus épsilon y delta, que no son más que números reales, muy pequeños y muy próximos a cero, y que tanto éxito le dieron.
La definición actual de límite como hemos podido comprobar, son el producto del esfuerzo combinado de grandes matemáticos, no hay que olvidar que ni siquiera Newton o Leibniz, considerados los padres del cálculo infinitesimal fueron capaces de intuirlo.
Límites matemáticos
Para la matemática, un límite es una magnitud a la que se acercan progresivamente los términos de una secuencia infinita de magnitudes. Un límite matemático, por lo tanto, expresa la tendencia de una función o de una sucesión mientras sus parámetros se aproximan a un cierto valor.
Una definición informal del límite matemático indica que el límite de una función f(x) es T cuando x tiende a s, siempre que se puede hallar para cada ocasión un x cerca de s de manera tal que el valor de f(x) sea tan cercano a T como se pretenda.
No obstante, además del límite citado, no podemos obviar que existen otros muy importantes en el ámbito de las Matemáticas. Así, también se puede hablar del límite de una sucesión que puede ser existente o único y divergente, en el caso de que los términos de aquella no converjan en ningún punto.
El concepto de límite es importante en análisis matemático; una herramienta básica para definir la derivada e integral definida, la existencia de número real al definir por un sistema de intervalos encajados, la potencia real de un real positivo. El plurimilenario caso de π, genial creatura de Arquímedes.
Límites de sucesión
El límite de una sucesión es el número al cual se van aproximando los términos de una sucesión.
El límite es 0.
a1= 0.5
a2= 0.6666....
a1000= 0.999000999001
a1000 000 = 0.999999000001
Límites de una Función
La expresión límite de una función se utiliza en el cálculo diferencial matemático y refiere a la cercanía entre un valor y un punto. Por ejemplo: si una función f tiene un límite X en un punto t, quiere decir que el valor de f puede ser todo lo cercano a X que se desee, con puntos suficientemente cercanos a t, pero distintos.
Límites Laterales
Definición de límite por la derecha | |
Se dice que
 si y solo si para cada  existe  tal que si entonces  es el límite por la derecha de  en "a". |
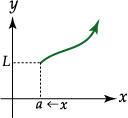
Observe que no hay barras de valor absoluto alrededor de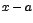 
, pues es mayor que cero ya que 
.
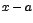, pues es mayor que cero ya que 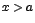.Definición de límite por la izquierda | |
Se dice que
 si y solo si para cada existe tal que si entonces  es el límite por la izquierda de en "a". |
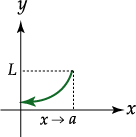
Análisis
- En matemáticas, la palabra Límite está asociada con la idea de aproximación entre números y el concepto de límite está estrechamente relacionado con la variación de los valores que toman las funciones o sucesiones.
- Se trata de un concepto maestro en el cálculo infinitesimal, un artefacto intelectual imprescindible para poder definir los conceptos fundamentales de convergencia, continuidad, derivación e integración, entre otros.
No hay comentarios.:
Publicar un comentario